我要学数学—PCA,LDA,NCA
一、PCA主成分分析法
一般的,有M个N维向量,将其变为由R个N维向量表示的新空间中,先将R个基按行组成矩阵A,然后将向量按列组成矩阵B,AB就是变换结果
1、在维规约的过程中,试图选择这样的一组基
1)希望投影后的投影值尽量分散,即投影后,字段的方差尽可能大
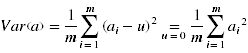
2)不希望第二个方向和第一个方向之间存在线性相关性,即使得投影后各字段协方差为0
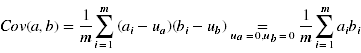
2、协方差矩阵
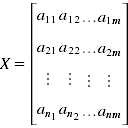 ,
,
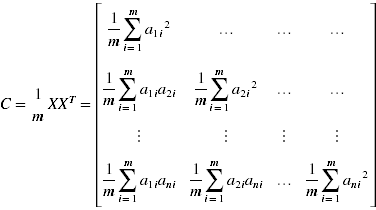
C是一个对称矩阵,其对角线分别是各个字段的方差,cij=cji为i和j字段的协方差
3、协方差矩阵的对角化
设P为一组基按行组成的矩阵,Y=PX为X对P做基变换后的数据,设D为Y的协方差矩阵
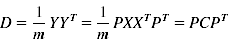
我们的优化目标是找到P,D为对角矩阵且对角线元素从大到小排列,P的前K行的转置就是要求的基。
已知若A是实对称矩阵,则存在同阶正交矩阵Q使得Q^TAQ是实对角矩阵
4、算法步骤
设有m条n维数据
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵C
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
二、LDA线性判别分析法
LDA的目标是,将带上标签的数据点,投影到维度更低的空间中,使得不同类别之间的距离远,同一类别之中的距离近
1、二值分类
将样例数据分类,就需要找到一个线性函数,我们将其表示为向量w,y=w^Tx即为将样本数据投影到w上的点
1)wi类样例的均值点(向量)
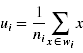
wi表示第i类元素的集合,ni表示wi中元素的个数,x即为样例,是一个向量,所以ui是一个向量
2)wi类样例投影到w后的均值点(标量)
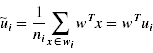
3)所有样例的均值点(向量)
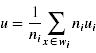
4)所有样例投影到w后的均值点(标量)
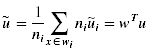
5)投影之后wi内部的方差(标量)
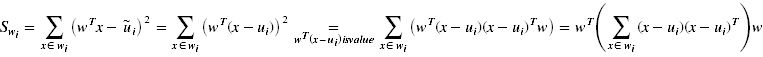
这里希望类内部的方差尽量小
6)投影之后类之间的方差(标量)
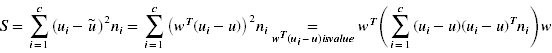
c表示数据一共可划分为c类,这里希望类之间的方差尽量大
于是我们记:
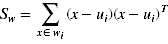
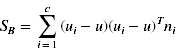
拉格朗日乘子法,限制
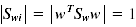
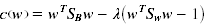
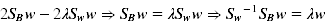
2、k-分类
由上述方法最多可以得到c-1个wi,每一个wi均可以将样例数据在其上做投影,因此记w=[w1|w2|……|wk](k<=c-1)。由于要求特征向量的矩阵不对称,所以w可能不正交。
三、NCA相邻成分分析
1、K最邻近算法(KNN)
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别
缺点:计算量较大,因为对每一个待分类的样本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点;模型设计时较难确定“最邻近”的概念
NCA是对KNN的改进
2、Distance Metric
首先定义Distance Metric,即两点之间距离的度量方式
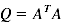
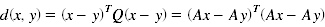
A是待优化的对象,通过A作用于x,y两点的坐标来度量x,y之间的距离
在这里,需要介绍一下向量范数的概念
向量范数是对三维欧式空间中向量长度概念的推广,距离的度量可以有多种定义方案,上述度量方案可视为一种R^n空间的向量范数:

我们有如下证明:

类似的,通过矩阵Q,我们定义了一个向量范数来度量两个数据点(向量)的距离
3、选择邻居的规则(随机选择)
每个点i选择另一个点j作为其邻居的概率为:
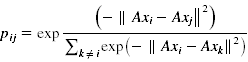
pi表示点i被正确分类的概率,Ci表示与i同类的点的集合:
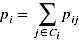
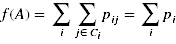
优化A,使得f(A)取得最大值,此时划分正确的概率最大,也就是被正确分类的样本个数的期望值最大,为了便于计算:
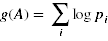
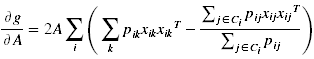
Obtaining a gradient for A means that it can be found with an iterative solver such as conjugate gradient descent.
四、参考资料
http://blog.csdn.net/xiaojidan2011/article/details/11595869
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html